Um grafo
G é dito ser euleriano
se há um ciclo em G
que contenha todas as suas arestas. Este
ciclo é dito ser um ciclo
euleriano. O grafo da
figura ao lado, por exemplo, é euleriano já
que ele contém o ciclo: (u1,
u2,
u3,
u4,
u5,
u3,
u6,
u7,
u1),
que é euleriano.
O
teorema que se segue provê um solução
simples para determinar que grafos e
multigrafos são eulerianos:
Teorema:
Um multigrafo M
é euleriano se e somente se M
é conexo e cada vértice de M
tem grau par.
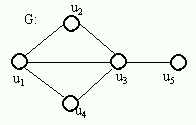Agora,
considere um multigrafo G
tenha uma trilha (não
um ciclo) contendo todas as arestas de M.
Então G é dito ser um grafo
atravessável e a trilha
é dita ser uma trilha
euleriana. No grafo ao
lado, a trilha: (u1,
u2,
u3,
u4,
u1,
u3,
u5)
é atravessável.
O
teorema seguinte indica precisamente que
grafos são atravessáveis:
Teorema: Um
multigrafo M é
atravessável se e somente se M
é conexo e tem exatamente dois vértices
de grau impar. Consequentemente, qualquer
trilha euleriana de M
começa em um dos vértices de grau impar
e termina no outro vértice de grau
impar.
Provavelmente,
o exemplo mais antigo de problema que faz uso
de grafos (ou conceito correlatos) como
modelo matemático é o Problema das Pontes
de Königsberg. Ele foi resolvido pelo
matemático suiço Leonhard Euler (1707-1783)
em 1736, a partir do qual gerou-se toda uma
classe de grafos que levam o nome de Euler.
No
século 18 havia na cidade de Königsberg
um conjunto de sete pontes (identificadas
pelas letras de a
até f
na figura ao lado ) que cruzavam o rio
Pregel . Elas conectavam duas ilhas
(A
e D)
entre si e as ilhas com as margens (B
e C).
Por
muito tempo os habitantes daquela cidade
perguntavam-se se era possível cruzar as
sete pontes numa caminhada contínua sem
que se passasse duas vezes por
qualquer uma delas.
Problema
do desenho da casa
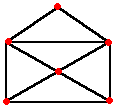
No
desenho ao lado, uma criança diz ter
posto a ponta do lápis numa das bolinhas
e com movimentos contínuos (sem levantar
e sem retroceder o lápis) traçou as
linhas que formam o desenho da casa,
traçando cada linha uma única vez.
A
mãe da criança acha que ela trapaceou
pois não foi capaz de achar nenhuma
seqüência que pudesse produzir tal
resultado. Você concorda com esta mãe?
O
Caso Count Van Diamond
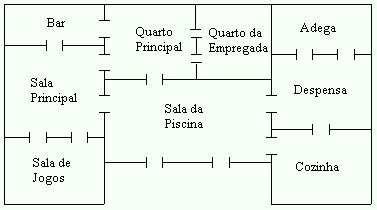
O
cenário ao lado é a residência do
bilionário Count Van Diamond, que acaba
de ser assassinado. Sherlock Gomes (um
conhecido detetive que nas horas vagas é
um estudioso da Teoria dos Grafos) foi
chamado para investigar o caso. O mordomo
alega ter visto o jardineiro entrar na
sala da piscina (lugar onde ocorreu o
assassinato) e logo em seguida deixar
sair daquela sala pela mesma porta que
havia entrado. O jardineiro, contudo,
afirma que ele não poderia ser a
pessoa vista pelo mordomo, pois ele havia
entrado na casa, passado por todas as
portas uma única vez e, em seguida,
deixado a casa. Sherlock Gomes avaliou a
planta da residência (conforme figura
abaixo) e em poucos minutos declarou
solucionado o caso. Quem poderia ser o
suspeito indicado por Sherlock Gomes?
Qual o raciocínio utilizado pelo
detetive para apontar o suspeito?
O
Problema da pavimentação de estradas
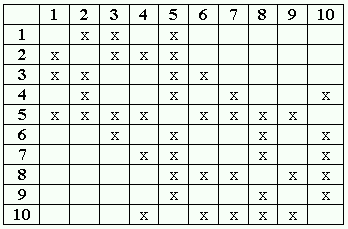
Tertuliano
Gonçalves havia prometido casamento a
Josefina das Graças. O evento
deveria ser realizado, segundo ele, assim
que acabasse o contrato de trabalho
recém assinado com uma empresa
encarregada de pavimentar toda a rede de
estradas que ligava Santana do Caixa
Prego (cidade onde morava Josefina)
às cidades da região. O trabalho
iria começar em Santana e prosseguir em
continuidade, estrada após estrada,
terminando, segundo explicou Tertuliano,
na própria Santana. A rede de estradas
é dada pela matriz de adjacência ao
lado, na qual a cidade de Santana
do Caixa Prego é representada pelo
número 1.
- Você que
leu esta estória acha que
Tertuliano estava sendo sincero
com Josefina? Por quê?
- E se o
itinerário 1-5-9-10 estivesse a
cargo de outra empresa, estaria
ele sendo sincero?
